Também era utilizado para resolver problemas geométricos, como calcular a altura de um edifício ou a profundidade de um poço. Era formado por disco de latão graduado na sua borda, num anel de suspensão e numa mediclina (espécie de ponteiro). O astrolábio náutico era uma versão simplificada do tradicional e tinha a possibilidade apenas de medir a altura dos astros para ajudar na localização em alto mar.
Se formos suficientemente engenhosos e irrequietos conseguimos de uma forma simples e prática, construir o nosso próprio astrolábio, ou pelo menos, o nosso próprio instrumento de medida de alturas.
Precisamos de:
- palhinha,
- transferidor, se não tiverem um imprimam o da imagem em papel grosso, cliquem ara aumentar,
- fio,
- anilha metálica, pode ser uma porca metálica grande,
- fita métrica,
- fita-cola.

- Cortem um pedaço de fio com cerca de 30cm;
- Atem a porca a uma das pontas do fio;
- Atem a segunda ponta exactamente no meio da parte recta do transferidor, podem usar a a fita métrica, mas em principio este centro está marcado o transferidor;
- Prendam a palhinha com fita cola ao transferidor, colem-na na parte recta do transferidor, como mostra a fotografia;
- Escolham um objecto alto, como uma árvore ou um prédio;
- Com a fita métrica meçam uma distância exacta, pode ser 5m, 10, 15... tem de ser o mais exacta possível, e quanto mais alto for o objecto mais ajuda se a distância for maior;
- Olhem através da palhinha;
- Deixe o irrequieto alinhar a palhinha com o topo do objecto que querem medir, como se fosse uma mira;
- Quando o seu irrequieto alinhar a palhinha faça a leitura do ângulo marcado no transferidor;
- Façam uma tabela no vosso "caderno de laboratório" com duas colunas, distância e ângulo;
- Anotem no vosso caderno o ângulo medido e a distância;
- Afastem-se mais alguns metros e repitam o procedimento;
- A cada medida anotem os dados na tabela;
- Façam 3 ou 4 medidas do mesmo objecto.
Agora apliquem a fórmula, e usem a tabela:
tg x= B
A
Em que x é o ângulo mediram no transferidor, A é a distância até ao objecto e B é a altura desconhecida do objecto.
Procurem na tabela seguinte o ângulo e o respectivo valor da tangente (tg).
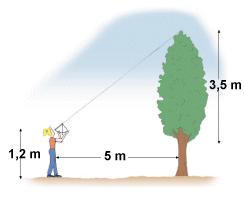
Vamos supor que a situação com que nos deparamos é a da imagem:
O ângulo que o transferidor marca é de 35º e a distância até à árvore é de 5m, quanto mede a árvore? o B?
Consultando a tabela a tangente de 35º é 0,7002, e a distância até à árvore é de 5m, ou seja:
tg x= B
A
tg 35= B
5
0,7002= B
5
B= 0,7002 x 5
B= 3,501m
Ou seja a altura da árvore, se o transferidor estivesse no chão era de 3,501m, como o temos na mão temos de adicionar a altura do chão aos olhos do irrequieto que o segura, neste caso 1,20m
Temos então que B=3,501+1,20 = 4,701m
Verificarão que à medida que se afastam do objecto, o ângulo diminui e consequentemente o valor da tangente também. Fazendo os cálculos para os valores que anotaram vão verificar que o tamanho da árvore é sempre o mesmo.
Não se deixem assustar com as fórmulas aparentemente complicadas! Esta é uma actividade que na realidade é bastante simples e depois de 2 ou 3 aplicações da fórmula os irrequietos já interiorizaram a fórmula.
Para além do mais, não vai ser um verdadeiro desafio calcular as alturas dos prédios e das árvores das redondezas?
Fontes:
http://www.museutec.org.br
http://www.brasilescola.com/matematica/seno-cosseno-tangente-angulos.htm
http://www.exatas.net/astrolabio.htm
Et voilá!
Matemática prática e divertida
Divirtam-se!








Sem comentários:
Enviar um comentário